# Strutture Dati ## Cos’è una Struttura di dati Una struttura di dati è una collezione di dati caratterizzata dalla struttura della collezione, piuttosto che dal tipo dei dati contenuti. Una struttura di dati è caratterizzata da un insieme di operatori che consentono di manipolarne la struttura e da un modo sistematico di organizzare i dati in essa contenuti. Le strutture di dati possono essere categorizzate sulla base di tre parametri: * Lineari/Non lineari: se è presente o meno una sequenza * Dinamiche/Statiche: se è possibile modificare o meno la dimensione della struttura dopo averla creata * Omogenee/Disomogenee: se i dati contenuti sono tutti dello stesso tipo o di tipi diversi ## Strutture dati Importanti ### Vettore Anche detto array, è una sequenza di dati **lineare** rappresentante una sequenza **ordinata** di valori che possono **comparire** anche **più di una volta**. La lunghezza del vettore non è mutabile. Se viene creato di 7 elementi non posso inserire 8 elementi. <im> Con la dicitura "sequenza ordinata" si intende che i valori hanno una loro **posizione specifica**, non che i valori sono contenuti e ordinati in un qualche ordine crescente o decrescente. </im> #### Operazioni ammesse Su un vettore sono ammesse le seguenti operazioni: * Accesso diretto a qualsiasi elemento conoscendone la posizione (posso accedere all’elemento in posizione 5 senza dover scorrere i precedenti) * Accesso sequenziale alle altre posizioni #### Vettori particolari - Matrici È possibile creare un vettore di vettori. Questa struttura dati si chiama generalmente **matrice** e la si può intendere come una **tabella**. Quella che si vede qui in esempio è una matrice quadrata. 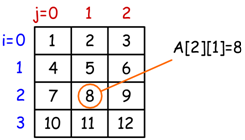<rt>  </rt> ### Set È un tipo di dato che rappresenta l’insieme matematico. Un set è una struttura dati **dinamica** e **non lineare** che memorizza una collezione **non ordinata** di valori **non ripetuti**. L'ordinamento fra elementi è dato dall'eventuale relazione d'ordine definita sul tipo degli elementi stessi. Ovvero, se usiamo un set contenente valori interi, l’ordine sarà definito dal metodo di confronto utilizzato per i numeri interi (generalmente quindi il valore 5 sarà posizionato prima del valore 7\) #### Operazioni ammesse Su un insieme sono ammessi diversi tipi di operazioni: * Inserimento di un valore * Rimozione di un valore * Test di appartenenza (verificare se un dato valore è presente nell’insieme o meno) * Estrazione valore massimo/minimo * Unione tra due set (insiemistica, quindi senza ripetizioni) * Intersezione tra due set * Differenza tra due set ### Dizionario Un dizionario è una struttura dati **dinamica** che rappresenta il concetto matematico di relazione univoca, o associazione **chiave-valore**, $R : D → C$, dove $D$ è un l'insieme dominio i cui elementi sono detti chiavi e $C$ è un insieme codominio di elementi detti valori. Lo si può intendere letteralmente come si intende un dizionario nella lingua italiana. Ovvero una serie di parole associate ad una loro descrizione. La struttura dati dizionario, a differenza del dizionario italiano, permette di usare come chiavi vari tipi di dato primitivo e come valori qualunque tipo di dato. #### Operazioni ammesse Su un dizionario sono ammesse le seguenti operazioni: * Data una chiave è possibile accedere al valore associato o a *null* se la chiave non è associata a nulla * Creazione di una nuova associazione chiave-valore, eventualmente sostituendo il precedente valore associato a quella chiave * Eliminazione di un'associazione chiave-valore ### Lista Una lista è una sequenza di **nodi** **contenenti** il **valore** effettivo e un **puntatore** all'elemento successivo (In certe implementazioni possono essere presenti due puntatori, uno al precedente ed uno al successivo). Diverse implementazioni di una lista possono essere categorizzate sulla base di tre parametri: * **Monodirezionali / Bidirezionali**: sono bidirezionali le implementazioni in cui ogni nodo contiene due puntatori: uno all'elemento precedente, l'altro al successivo. 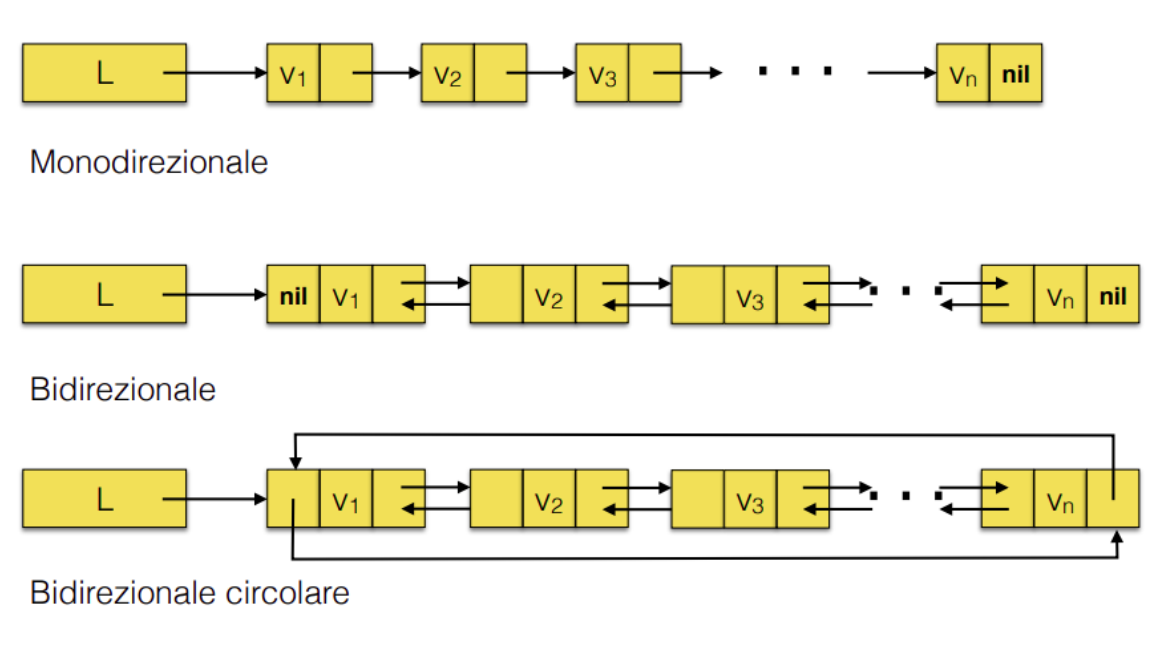si dicono bidirezionali perché consentono la consultazione veloce sia in una direzione che nell’altra * **Circolare / Non circolare**: sono circolari le implementazioni in cui l'ultimo elemento ha come successivo il primo, o viceversa  ### Pila Una pila (Stack) è una struttura dati **dinamica** e **lineare**, nella quale l'accesso agli elementi è definito in base all'**ordine** in cui sono **stati inseriti**. In particolare, è possibile accedere direttamente soltanto all'**ultimo** elemento inserito. Le pile sono basate sull'approccio LIFO (Last In, First Out). 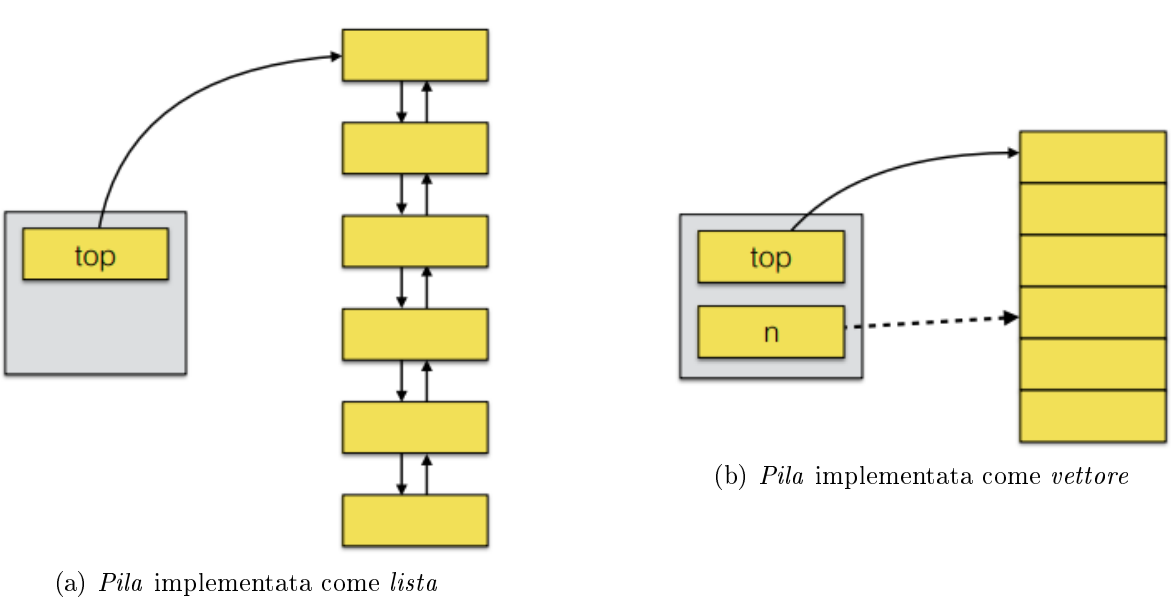Può essere implementata basandosi su altre strutture dati, ad esempio vettori o liste  ### Coda <lf> Una coda (Queue) è una struttura dati **dinamica** e **lineare**, nella quale l'accesso agli elementi è definito in base all'**ordine** in cui sono **stati inseriti**. In particolare, è possibile accedere direttamente soltanto al **primo** elemento inserito. Le code sono basate sull'approccio FIFO (First In, First Out) e rappresentano esattamente quello che si intende normalmente per coda (o fila), ad esempio la coda al supermercato. Come per la lista, può essere implementata basandosi su altre strutture dati, ad esempio liste. Qui possiamo vedere la differenza tra pila e coda. 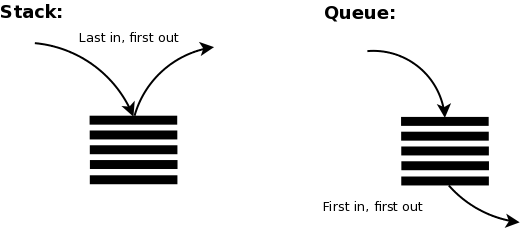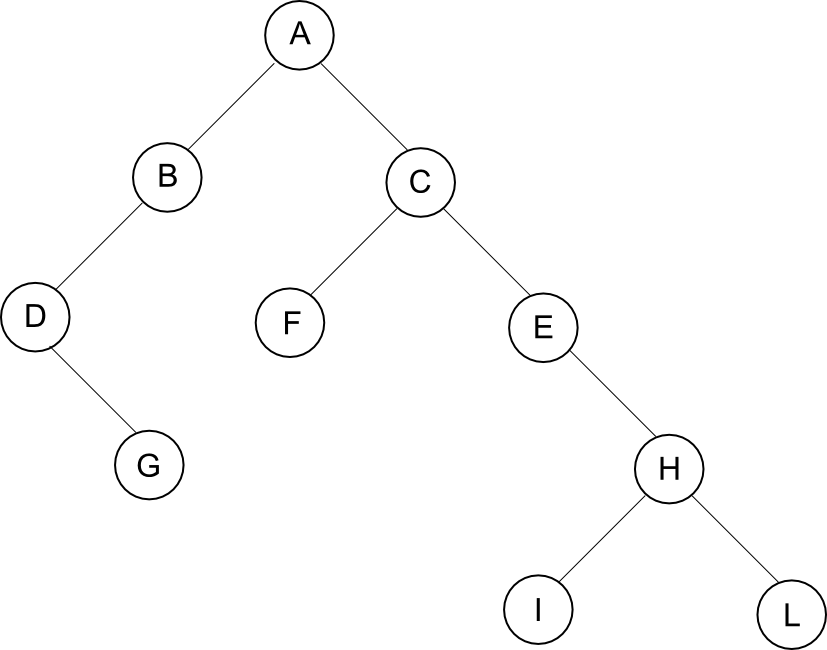</lf> <rt>  </rt> ### Albero <lf> È una struttura dati **gerarchica** composta da **nodi** collegati tra loro da **archi** in modo simile a una struttura ad albero reale. Ogni nodo in un albero può avere uno o più nodi figli, ad eccezione del nodo radice che è il punto di partenza dell'albero. Gli alberi vengono utilizzati per organizzare e rappresentare dati in una gerarchia logica. Generalmente in programmazione tornano molto utili gli alberi binari, ovvero alberi in cui ogni nodo ha due figli (entrambi potenzialmente nulli). #### Proprietà * Un nodo dell'albero è designato come nodo **radice** * Ogni nodo n, a parte la radice, ha **esattamente un arco entrante** * Per ogni nodo esiste un unico cammino che parte dalla radice e raggiunge quel nodo * È definita **profondità** di un nodo la lunghezza del cammino semplice dalla radice al nodo. La lunghezza è misurata in numero di archi attraversati * È definito **livello** l'insieme dei nodi alla stessa profondità * È definita **foglia** un nodo che non ha archi uscenti (non ha nodi sotto di lui) * È definita **altezza** di un albero la profondità massima della sue foglie * Un albero è detto **bilanciato** se tutte le foglie hanno uguale profondità dalla radice </lf> <rt>  </rt> ### Alberi Binari di Ricerca  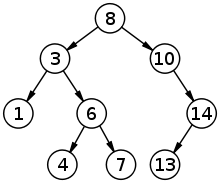Un albero binario di ricerca (BST, Binary Search Tree) è una struttura dati che organizza i dati in modo **gerarchico**. In un BST, ogni nodo contiene un valore unico e ha al massimo due figli: un figlio sinistro e un figlio destro. La proprietà fondamentale di un BST è che, per ogni nodo, tutti i valori nel sottoalbero sinistro sono minori del valore del nodo, mentre tutti i valori nel sottoalbero destro sono maggiori del valore del nodo. Questa proprietà permette di effettuare ricerche, inserimenti e cancellazioni in **modo efficiente**, seguendo una logica di confronto che **dimezza** il cammino medio **ogni volta**, simile alla ricerca binaria in un array ordinato. Il tempo di ricerca, inserimento e cancellazione in un BST, in media, tende a essere *logaritmico* rispetto al numero di nodi, ovvero $O(\log{n})$, se l'albero è bilanciato. Un albero sbilanciato, tuttavia, può degenerare in una lista collegata, con operazioni che possono richiedere tempo lineare, ovvero $O(n)$. Per questo è importante creare delle regole per mantenere l’albero il più possibile bilanciato. ### Grafo Un grafo è una coppia $G = (V, E)$ dove V è l'insieme dei vertici (o dei nodi) del grafo ed E è un insieme di coppie di nodi $(u, v)$ per $u, v ∈ V$ dette archi. Possiamo vedere un grafo come un albero nel quale ogni nodo può **avere più nodi entranti**. Per la memorizzazione dei grafi si ricorre spesso a **matrici** di adiacenza o a **liste** di adiacenza. 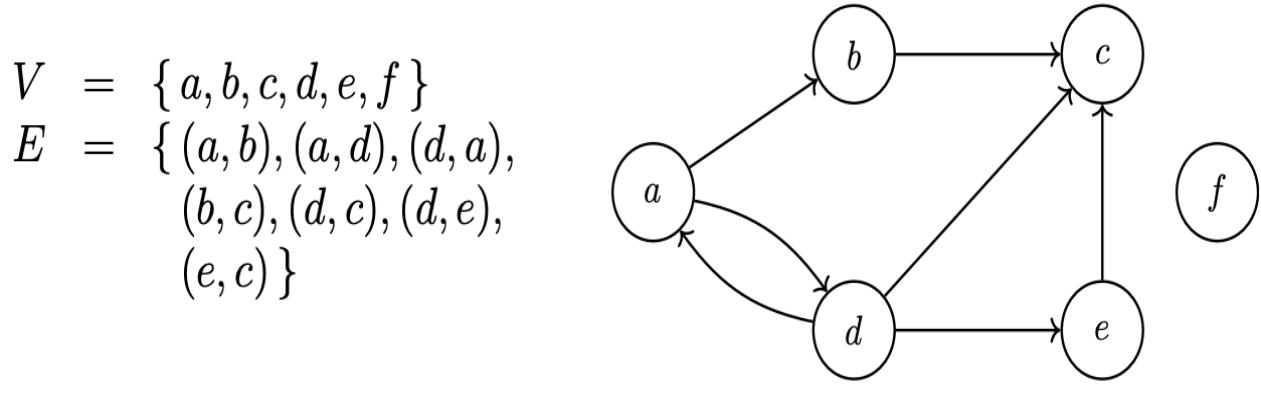I grafi si distinguono in due macro tipi: #### Grafi orientati  Ogni arco ha una direzione. Il nodo *a* può andare a *b* mentre *b* non può andare ad *a.* Il numero di archi massimi in un grafo orientato è $m \lt n(n-1)$. Ovvero ogni nodo ha un arco con ogni altro nodo eccetto se stesso. 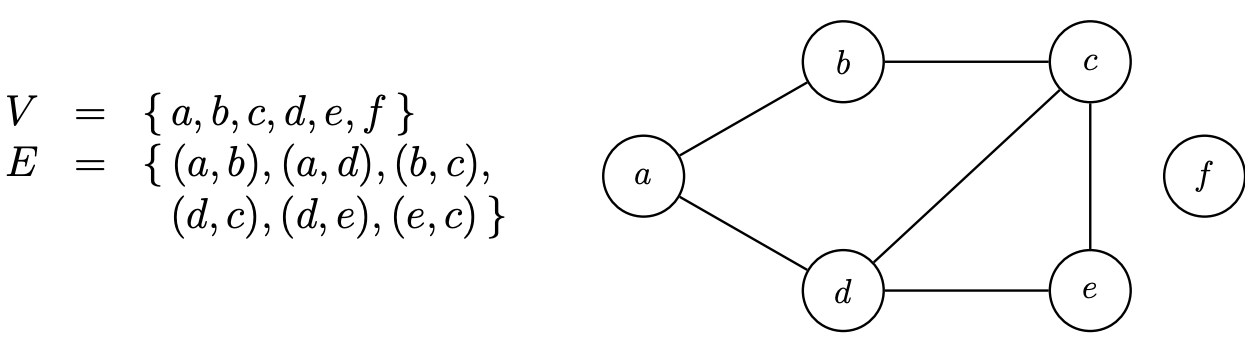#### Grafi non orientati  Se esiste l’arco *(a,b)* allora *a* può andare a *b* e *b* può andare ad *a*. Il numero di archi massimi in un grafo non orientato è $m \lt n(n-1) / 2$. Ovvero ogni coppia di nodi (tranne quelle banali) ha un arco.