# Database - Operazioni Relazionali In generale gli **operatori relazionali** agiscono su una o più relazioni per ottenere una nuova relazione. In sostanza le operazioni relazionali consentono di effettuare le interrogazioni alla base di dati per ottenere le informazioni desiderate estraendo da una tabella una sottotabella, oppure combinando tra loro due o più tabelle e generando così nuove relazioni. Con le operazioni relazionali si costruiscono le espressioni dell’**algebra relazionale**, strumento di fondamentale importanza per comprendere come si interrogano i database relazionali. Si tratta di uno strumento teorico perché le espressioni dell’algebra relazionale non sono usate esplicitamente dai DBMS commerciali. Sono però alla base delle strategie da usare per interrogare i database. ## Selezione, proiezione e congiunzione Le principali operazioni relazionali sono la **selezione**, la **proiezione** e la **congiunzione**. Selezione e proiezione agiscono su una sola tabella, a differenza della congiunzione che agisce su due tabelle. La selezione è un’operazione che estrae da una tabella solo alcune righe, mentre la proiezione è un’operazione che estrae solo alcune colonne. ### Proiezione La **proiezione** su una tabella T genera una nuova tabella estraendo dalla tabella iniziale solo le colonne elencate nella lista L. La proiezione è indicata con la scrittura: $\pi\_{L}(T)$ dove il simbolo di proiezione $\pi$(pi greco) è seguito dal nome della tabella **T** sulla quale viene operata la proiezione. La lista **L**, che elenca le colonne da estrarre da **T**, viene riportata come indice di $\pi$. La tabella ottenuta da un’operazione di proiezione è caratterizzata da: * grado minore o uguale al grado della relazione di partenza (il grado è uguale a quello di partenza nel caso di una proiezione effettuata allo scopo di ottenere una tabella con le colonne riordinate); * cardinalità minore o uguale a quella di partenza, anche se nella maggior parte dei casi è uguale a quella di partenza. È minore se, per effetto della proiezione su un numero di colonne minore di quello originale, si ottiene una tabella con righe uguali: in questo caso le righe duplicate diventano una sola perché il modello relazionale richiede, come è stato detto in precedenza, che le righe di una tabella siano tutte distinte. 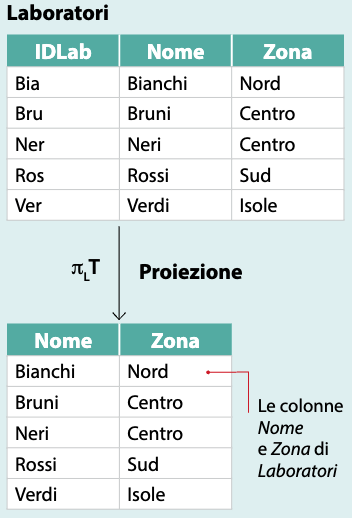<ex>  </ex> ### Selezione La **selezione** su una tabella T genera una nuova tabella costituita solo dalle n-uple della tabella di partenza che soddisfano una determinata condizione **P**. La selezione viene indicata con la scrittura: $\sigma\_{P}(T)$ dove il simbolo di selezione $\sigma$(sigma) è seguito dal nome della tabella **T** sulla quale viene operata la selezione. La proprietà **P**, che caratterizza l’operazione di selezione, viene scritta come indice di $\sigma$. La scrittura $\sigma\_{P}(T)$ indica quindi un'operazione su **T** che estrae le sole righe per le quali la proprietà **P** è vera. La tabella ottenuta da un’operazione di selezione è caratterizzata da: * **grado** uguale al grado di T, poiché la tabella ottenuta ha tutte le colonne di T; * **cardinalità** che può essere minore o uguale alla tabella di partenza, ma è ragionevole pensare che sia solitamente minore. La cardinalità è uguale quando tutte le righe di T soddisfano la condizione P. 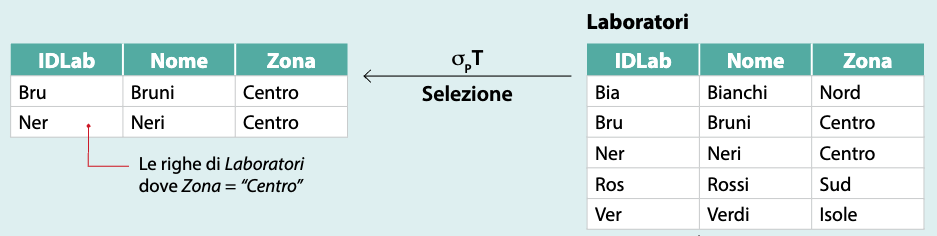<ex>  </ex> ### Congiunzione La congiunzione tra due tabelle *R* e *S*, di schema *R(A1, A2, ... Am)* e *S(B1, B2, ... Bn)*, combina le due relazioni generando una nuova tabella le cui righe contengono tutti gli attributi di *R* e di *S* abbinando le sole righe di R e di S che soddisfano una data proprietà *P*. Nella sua forma più generale la congiunzione di R e S si indica con: $ R \Join PS $ dove $\Join$ è il simbolo di congiunzione e si legge **join**. In Pratica, nella maggior parte dei casi, la proprietà *P* consiste in una o più condizioni di uguaglianza tra attributi di *R* e attributi di *S*: $R.Aj =S.Bk$ Nel caso ci siano più condizioni di uguaglianza, le diverse condizioni sono composte con operatori logici, nella maggior parte dei casi con AND: $$ R.Aj \= S.Bk \text{ AND } R.Ar \= S.Bs $$ Questo tipo di congiunzione è indicato con il nome di **equi-join**. La relazione risultante da una congiunzione ha le seguenti caratteristiche. * Se il grado (cioè il numero delle colonne) delle relazioni *R* e *S* è, rispettivamente, *m* e *n*, il **grado** della congiunzione è *m+n*. * Nel caso di join generici la **cardinalità** della relazione risultante non è prevedibile a priori e si può solo dire che il numero di righe della relazione risultante è minore o uguale (in genere minore) al prodotto del numero di righe di *R* per il numero di righe di *S*. L’equi-join produce una relazione con informazioni ridondanti, in quanto la colonna (o le colonne) che sono confrontate per ricercare valori identici è duplicata. La congiunzione che evita tale ridondanza si chiama **join naturale**. Nel join naturale sono combinate le sole righe delle due tabelle con valori identici negli attributi comuni (con lo stesso nome) che sono presenti una sola volta nelle righe della congiunzione. Il join naturale tra *R* e *S* ha le seguenti caratteristiche. * Se il grado delle relazioni *R* e *S* è *m* e *n* e le due tabelle hanno *k* attributi comuni, allora *R join S* ha **grado** uguale a *m+n-k*. * Per la cardinalità di *R* join *S* valgono le considerazioni già svolte per l’equi-join. Il join naturale viene indicato con il simbolo ⋈ posto tra le due relazioni R e S che sono combinate. 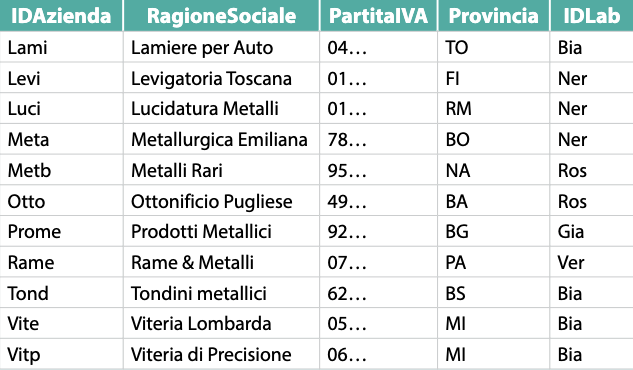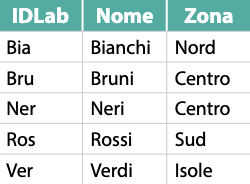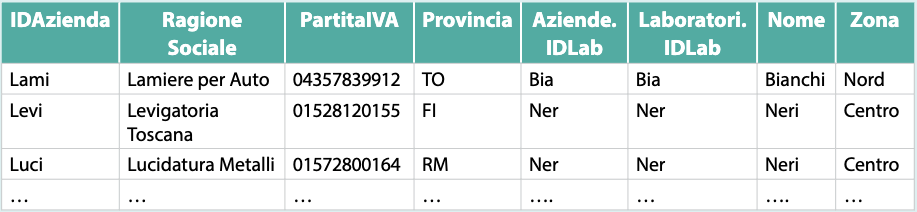L’attributo A, comune alle due tabelle, è riportato come indice dei nomi delle tabelle: $ R_{A} ⋈ S_{A}$ <ex> Applicazione della congiunzione $ \text{Aziende.IDLab} \= \text{Laboratori.IDLab}$ partendo dalle seguenti tabelle: **Aziende**  **Laboratori**  **Aziende ⋈ Laboratori** $ R \Join _{ \text{Aziende.IDLab} = \text{Laboratori.IDLab}} S $  </ex> ## Operazioni Insiemistiche Sulle tabelle si possono eseguire le operazioni insiemistiche di **unione**, **intersezione** e **differenza** che permettono di combinare due relazioni R e S, di identico schema (con attributi uguali in nome e numero), costruendo le seguenti relazioni. - L'**unione** di *R* e *S*, indicata con la scrittura $R ∪ S$, è formata dalle righe presenti in *R* oppure in *S*. - L'**intersezione** di *R* e *S*, indicata con $R ∩ S$, è formata dalle righe comuni a *R* e *S*. - La **differenza** tra *R* e *S*, indicata con $R - S$, è formata dalle righe di *R* che non sono presenti in *S*.