# Apprendimento Non Supervisionato ## Cos'è l'apprendimento non supervisionato? L'apprendimento non supervisionato è un tipo di machine learning in cui l'algoritmo apprende dai dati **senza etichette di riferimento**. L'obiettivo è quello di esplorare e **scoprire strutture o schemi nascosti** nei dati. Questo tipo di apprendimento è utile quando si ha a disposizione una grande quantità di dati ma non si conoscono le relazioni tra le variabili o le categorie a cui appartengono gli esempi. **Applicazioni tipiche**: - Analisi dei dati per scoprire pattern nascosti. - Raggruppamento di utenti o clienti con comportamenti simili per strategie di marketing mirate. - Rilevamento di anomalie, come transazioni sospette nelle attività bancarie. ## Clustering: un focus specifico Una delle tecniche più comuni e rilevanti dell'apprendimento non supervisionato è il **clustering**, che consiste nel raggruppare i dati in insiemi (cluster) in modo tale che i dati all'interno dello stesso cluster siano simili tra loro e diversi dai dati appartenenti ad altri cluster.  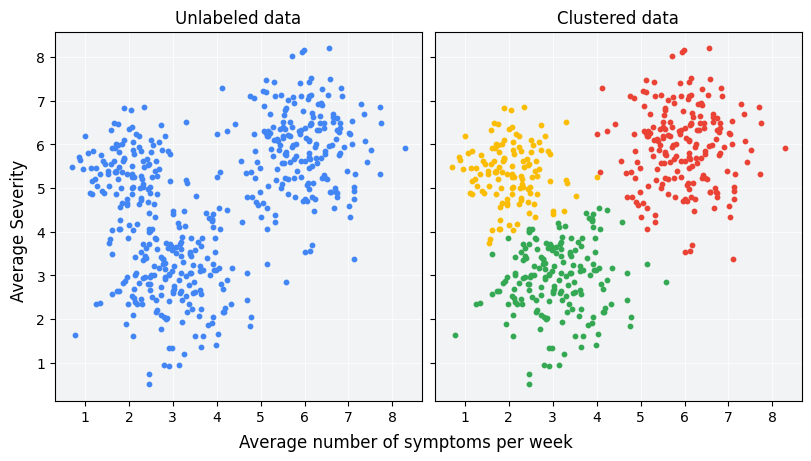## Esempi Concreti di Utilizzo del Clustering ### Clustering per Sistemi di Raccomandazione I sistemi di raccomandazione utilizzano il clustering per offrire contenuti personalizzati agli utenti. In un sistema di streaming, ad esempio, possiamo utilizzare il clustering per identificare gruppi di utenti con preferenze simili, in modo da raccomandare film o serie TV in base ai gusti di ciascun cluster. **Esempio pratico**: Immaginiamo di avere dati sugli utenti di una piattaforma di streaming, inclusi film visti, generi preferiti, tempo di visione e rating dato ai contenuti. Utilizzando l'algoritmo **K-Means**, potremmo suddividere gli utenti in diversi gruppi: - **Cluster 1**: Appassionati di film d'azione e thriller. - **Cluster 2**: Amanti di serie drammatiche e storiche. - **Cluster 3**: Utenti che preferiscono documentari e film biografici. Una volta identificati questi cluster, il sistema può raccomandare nuovi contenuti agli utenti basandosi sulle preferenze del loro cluster di appartenenza. Se un nuovo documentario viene aggiunto alla piattaforma, questo verrà suggerito agli utenti del Cluster 3, mentre una nuova serie d'azione sarà raccomandata al Cluster 1. Questo approccio permette di migliorare l'esperienza utente senza analizzare le singole preferenze in modo dettagliato, sfruttando invece i dati aggregati dei cluster. ### Clustering per la Compressione dei Dati Il clustering può essere utilizzato anche per ridurre la dimensione dei dati, quindi per la compressione. Un esempio classico è la **compressione delle immagini**, dove i colori simili possono essere rappresentati come un singolo cluster di pixel, riducendo così il numero complessivo di colori e comprimendo l'immagine. **Esempio pratico**: Immagina un’immagine digitale ad alta risoluzione che contiene milioni di colori leggermente diversi. Utilizzando un algoritmo come **K-Means**, possiamo raggruppare i colori simili in un numero limitato di cluster (ad esempio, 64 cluster). Ogni cluster rappresenta un colore centrale, e tutti i pixel appartenenti a un certo cluster vengono rappresentati con quel colore. In questo modo, l’immagine finale contiene solo 64 colori distinti anziché milioni, riducendo significativamente la dimensione del file. Anche se l'immagine risulterà leggermente meno dettagliata, la differenza potrebbe essere quasi impercettibile per l'occhio umano. ### Clustering per la Sicurezza Immagina un sistema di sorveglianza che monitora una zona pedonale. Durante la giornata, la videocamera registra il normale movimento delle persone che camminano e, occasionalmente, qualche bicicletta. Usando il clustering, il sistema "impara" questi comportamenti abituali e crea dei gruppi, o "cluster", di movimenti tipici. Ora, se un motorino attraversa la zona pedonale a una velocità anomala, il sistema riconosce subito che questo comportamento non rientra nei cluster usuali. Poiché si tratta di un movimento insolito, il sistema segnala l’evento come potenzialmente sospetto. Questo approccio permette di rilevare automaticamente **situazioni fuori dall’ordinario**, come il passaggio di un veicolo in un’area pedonale, e di avvisare tempestivamente il personale di sicurezza. Queste situazioni "fuori dall'ordinario" prendono il nome di **outlier**, vedremo più avanti cosa sono. ### Clustering per la Segmentazione del Mercato Nel marketing, il clustering viene utilizzato per segmentare i clienti in gruppi con comportamenti di acquisto simili, per ottimizzare le strategie pubblicitarie e personalizzare le offerte. **Esempio pratico**: Immaginiamo una catena di negozi che raccoglie dati sugli acquisti dei clienti, come prodotti acquistati, frequenza degli acquisti e importo speso. Utilizzando un algoritmo di clustering come **Mean Shift** o **Agglomerative Clustering**, è possibile segmentare i clienti in gruppi, ad esempio: - **Cluster 1**: Clienti che fanno acquisti frequenti ma con importi bassi. - **Cluster 2**: Clienti che acquistano occasionalmente ma spendono cifre elevate. - **Cluster 3**: Clienti che acquistano regolarmente prodotti di una categoria specifica, come l'abbigliamento sportivo. Queste informazioni permettono al team di marketing di personalizzare le campagne pubblicitarie per ogni cluster. Ad esempio, i clienti del Cluster 1 possono ricevere promozioni sugli acquisti di piccolo importo, mentre ai clienti del Cluster 2 possono essere offerte sconti su prodotti premium. In questo modo, la segmentazione dei clienti permette di migliorare l'efficacia delle campagne pubblicitarie. ### Clustering per l'Analisi dei Dati Biomedici Nel settore medico e biomedico, il clustering è utilizzato per identificare gruppi di pazienti con sintomi simili, aiutando a diagnosticare e trattare malattie con caratteristiche comuni. **Esempio pratico**: Supponiamo di avere un dataset che raccoglie informazioni su pazienti con sintomi di malattie respiratorie, come febbre, tosse, difficoltà respiratorie e altri parametri medici. Utilizzando un algoritmo come **Hierarchical Clustering**, è possibile suddividere i pazienti in cluster che rappresentano gruppi con sintomi simili. Ad esempio: - **Cluster 1**: Pazienti con sintomi leggeri, come tosse e mal di gola. - **Cluster 2**: Pazienti con sintomi moderati, come febbre e difficoltà respiratorie. - **Cluster 3**: Pazienti con sintomi gravi, come insufficienza respiratoria. Questa segmentazione può aiutare i medici a identificare pattern comuni nei pazienti e a sviluppare protocolli di trattamento specifici per ogni cluster. Inoltre, il clustering può essere usato per scoprire nuove correlazioni tra sintomi e malattie, fornendo spunti per nuove ricerche mediche. ### Clustering per la Gestione delle Scorte Nella gestione delle scorte, il clustering può essere utilizzato per raggruppare i prodotti in base a caratteristiche come frequenza di vendita, stagionalità o volumi di acquisto, aiutando a ottimizzare l'inventario. **Esempio pratico**: Immaginiamo che un magazzino venda migliaia di prodotti diversi. Utilizzando il clustering, possiamo identificare gruppi di prodotti con comportamenti simili, ad esempio: - **Cluster 1**: Prodotti con domanda costante tutto l’anno. - **Cluster 2**: Prodotti stagionali, come decorazioni natalizie. - **Cluster 3**: Prodotti a rotazione rapida, che devono essere riforniti frequentemente. Questi cluster permettono di adottare strategie di gestione delle scorte più mirate, come l’ordinazione anticipata per i prodotti stagionali o la riduzione dell'inventario per prodotti con bassa domanda. In questo modo, l'azienda può ottimizzare il magazzino, ridurre i costi di stoccaggio e migliorare la disponibilità dei prodotti. ## K-Means: il clustering in dettaglio Uno degli algoritmi più utilizzati per il clustering è il **K-Means**. È semplice da implementare ed efficace per molte applicazioni di raggruppamento. L'algoritmo K-Means funziona suddividendo i dati in un numero *k* di cluster predefiniti. Vediamo come funziona in dettaglio.  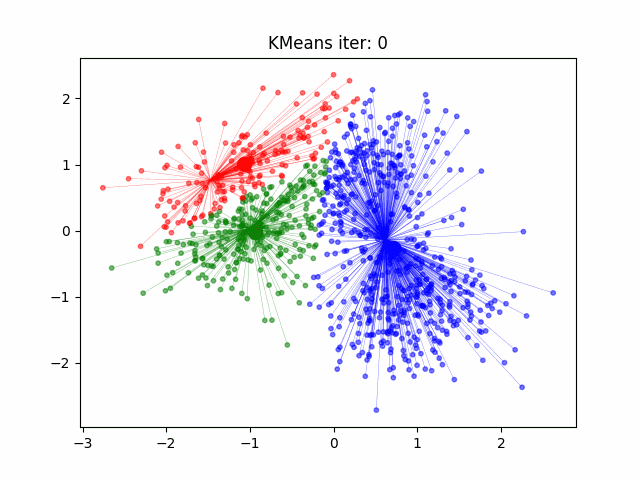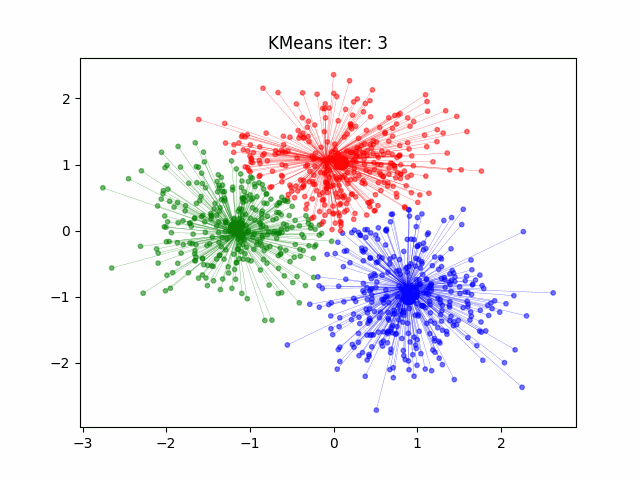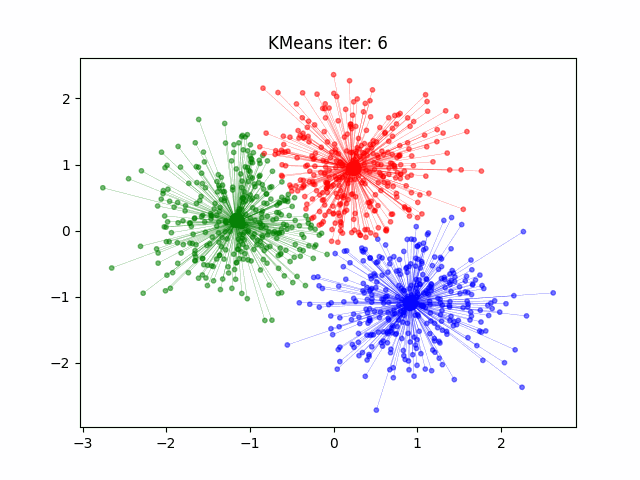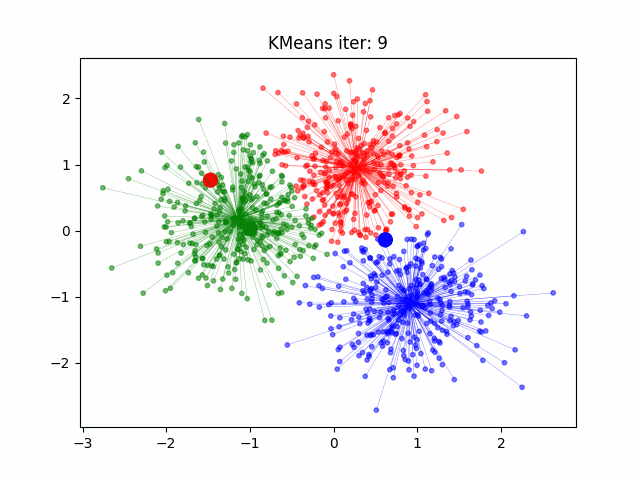**Funzionamento di K-Means**: 1. **Inizializzazione**: Si scelgono casualmente *k* **centroidi**, che rappresentano i punti iniziali per i cluster (i *k* centri iniziali dei cluster). 2. **Assegnazione dei punti**: Ogni punto del dataset viene assegnato al centroide più vicino, formando così *k* cluster iniziali. 3. **Ricalcolo dei centroidi**: Per ogni cluster, si calcola il nuovo centroide come il punto medio tra i punti assegnati a quel cluster. 4. **Ripetizione**: Si ripete il processo di assegnazione dei punti e ricalcolo dei centroidi finché i centroidi non cambiano più o il cambiamento è minimo. Questo significa che i cluster si sono stabilizzati. **Esempio pratico**: Immaginiamo di avere un dataset con le caratteristiche di diversi clienti, come l'età e la spesa media mensile. Utilizzando K-Means con *k=3*, l'algoritmo dividerà i clienti in tre gruppi distinti, ciascuno con un centroide che rappresenta la media delle caratteristiche dei clienti in quel gruppo. Questo permette di identificare cluster come "giovani con spese basse", "adulti con spese medie" e "anziani con spese alte". **Vantaggi di K-Means**: - **Semplicità**: Facile da implementare e computazionalmente efficiente, specialmente per dataset di dimensioni moderate. - **Velocità**: La convergenza è rapida e l'algoritmo è in grado di processare grandi quantità di dati in tempi ragionevoli. - **Interpretazione chiara**: I cluster formati sono intuitivi da interpretare e rappresentano gruppi omogenei. **Limitazioni di K-Means**: - **Sensibilità ai centroidi iniziali**: La scelta iniziale dei centroidi può influenzare notevolmente il risultato finale. Un modo per mitigare questo problema è eseguire l'algoritmo più volte con diverse inizializzazioni. - **Numero di cluster predefinito**: L'algoritmo richiede che il numero *k* di cluster sia specificato in anticipo, il che può essere difficile da determinare senza una conoscenza preliminare dei dati. - **Assunzione di forma sferica**: K-Means tende a formare cluster sferici e non è adatto per cluster di forma complessa o con densità variabile.